
趣味で算数
趣味で勉強をしてみると、強制では感じられない楽しさの発見があります。
今回は、自分のお気に入りの問題を紹介したいと思います。
時間のある人は、紙と鉛筆を用意して考えてみてください。
問題
影となっている部分の角度の和(合計)を求めてください。

ヒントと一言
内角や外角の関係を上手く使ってください。
とりあえず分度器を使っても構いませんよ。
お約束の一言ですが、この問題を作った人、あんたすごいよ!
解答
解答の前に、知っておくべき定理が2つあります。
一つ目は、三角形の内角の和が180°になることです。
便宜上、内角定理と呼ぶことにします。
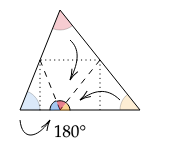
上図のように上手く折り返すと、ちょうど180°になることが確認できると思います。
二つ目は、2つの内角の和は隣り合わない1つの外角と等しいことです。
これは外角定理と呼ぶことにします。

緑の点線で表した平行な補助線を引いて、錯覚と同位角を考えれば納得できると思います。
以上の内角定理と外角定理を押さえた上で問題の解説に移ります。
まず、赤の三角形に注目して外角定理を使うと、薄い赤の角度の和は濃い赤になります。

同様に、青の三角形に注目して外角定理を使うと、薄い青の角度の和は濃い青になります。

これらを まとめたのが次の図です。

もう おわかりでしょうが、最後に内角定理を使うと、求める角度の和は180°となります。
あとがき
いわゆる五芒星の角度の和は、一つひとつが分からなくても180°になるところがスゴイと思います。
中学生は「五芒星の角度の和は180°」と覚えておくとテストに出るかも。
他に、角度がらみの問題は次のようなものがあります。
絵ばっかり描いていて埋もれてしまっているのですが、算数の記事も ときどき書いています。
算数好きな方はグローバルメニュー(最上部)から一覧が見られます。
